Méthodes de régressions avancées

Julien Duval
R , Data
6 avril 2022

Sommaire

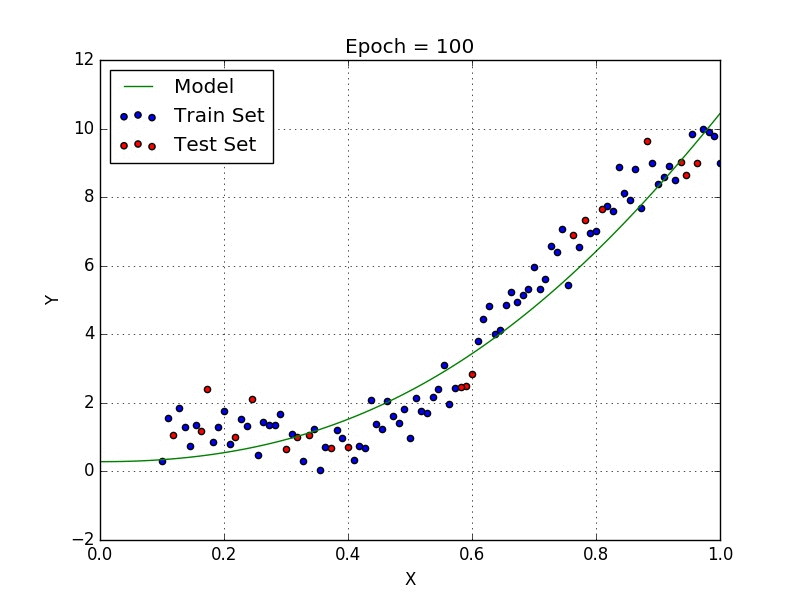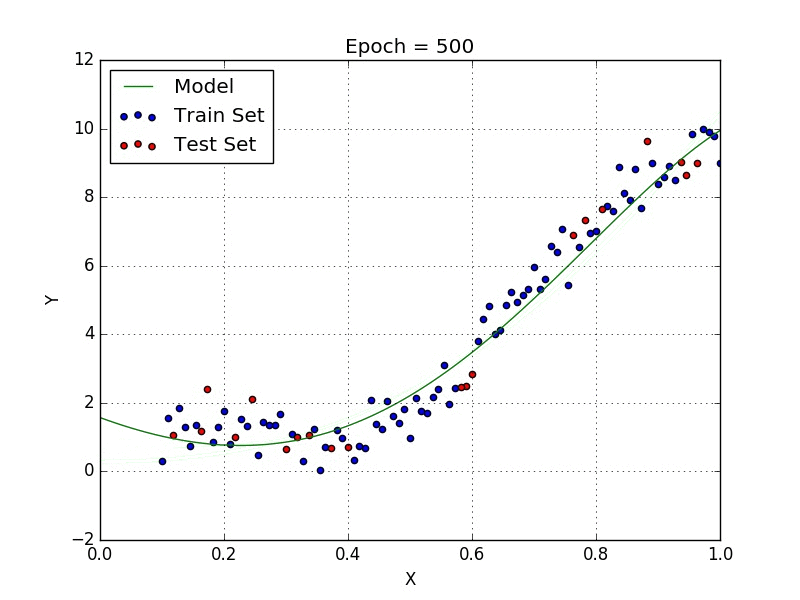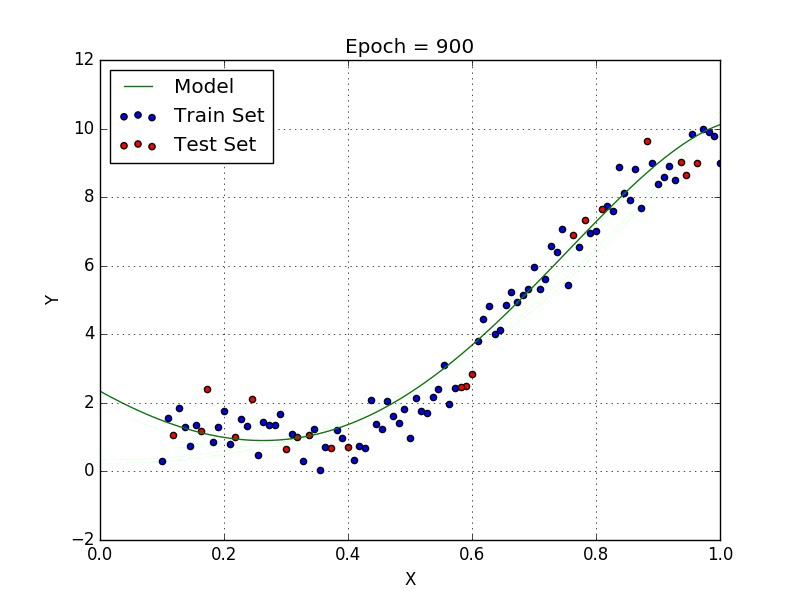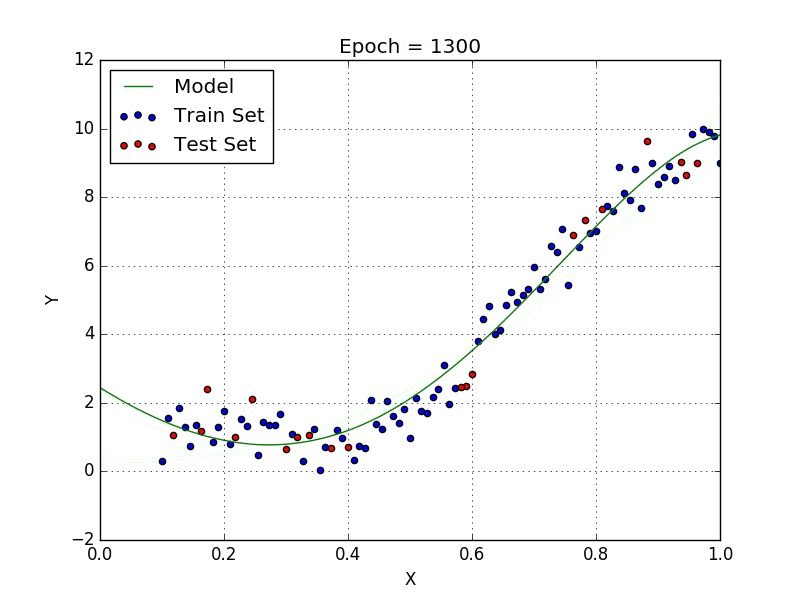
Construire un modèle robuste et généralisable capable de prédire y pour des données inconnues (Xtest) en explorant et en comparant plusieurs approches modernes de régression.

Info

Ingénierie des caractéristiques et régularisation des modèles
Analyse comparative des techniques de régression
Évaluation et optimisation des modèles basées sur la RMSE

Présentation du projet

Ce projet s’inscrivait dans le cadre du cours « Méthodes avancées de régression » et visait à construire le modèle prédictif le plus précis possible pour une variable cible y à partir de 100 variables explicatives x(1), …, x(100).

Le principal défi consistait à minimiser l’erreur de prédiction sur un ensemble de données de test (Xtest.txt), en utilisant l’erreur quadratique moyenne (RMSE) comme mesure d’évaluation.

Objectifs

Note

Développez un modèle de régression robuste et efficace capable de prédire la variable y à partir de 100 caractéristiques explicatives. Le modèle final doit générer 100 prédictions correspondant aux observations dans l’ensemble de données de test fourni.

Les étapes du projet

Chargement des données et exploration

Analyse descriptive de la variable cible yet des prédicteurs x(i)
Calacul d’un RMSE témoin en utilisant la moyenne des y

Sélection des modèles et tests

Régression Linéaire Multiple (MLR)
Régression Ridge
LASSO
Régression par Composantes Principales (PCR)
Partial Least Squares (PLS)
Stepwise Regression

Evaluation du modèle

Validation croisée pour comparer les performances entre les modèles
Sélection du modèle en se basant sur l’optimalité du RMSE

Prédictions finales

Application du modèle sélectionné à notre fichier Xtest.txt
Calcul et export des prédictions de la variable y dans un fichier NAME.txt

Outils & technologies utilisées

Tool	Purpose
Python / R	Data analysis and modeling
NumPy / Pandas	Data manipulation and preprocessing
scikit-learn	Implementation of regression models
matplotlib / seaborn	Visualization of results
statsmodels	Statistical modeling and diagnostics

La mesure de l’évaluation

Root Mean Squared Error (RMSE)

La formule du Root Mean Squared Error (RMSE) est donnée par :

$$ \text{RMSE} = \sqrt{\frac{1}{n_{\text{test}}} \sum_{i=1}^{n_{\text{test}}} (y_i - \hat{y}_i)^2} $$

Info

où :

$n_{\text{test}}$ est le nombre d’observations dans l’échantillon de test,
$y_i$ est la valeur réelle de l’observation $i$,
$\hat{y}_i$ est la valeur prédite correspondante.

Un RMSE bas signifie un model plus précis et un modèle plus stable.

Warning

Cependant, bien qu’un RMSE bas soit un objectif, nous devons faire attention à l’overfitting pour ne pas avoir un modèle trop fidèle aux données de test et ainsi très imprevisible dans ses prédictions.

Résultats

Quote

LE RMSE de programme est de 2,947 ! Soit une différence de 0,02 du professeur référent et de ses prédictions.

Nous pouvons donc en conclure que notre modèle bien que perfectible fourni une prédiction très satisfaisant au regard des données fournies.

Compétences développées

Maîtrise des techniques avancées de régression
Traitement des données multivariées à grandes dimensions
Application de la régularisation et de la réduction de dimensionnalité
Optimisation des modèles sur la base de critères de performance quantitatifs
Communication claire des résultats analytiques et de la méthodologie

Le code

import numpy as np
import pandas as pd
from sklearn.model_selection import GridSearchCV, train_test_split
from sklearn.metrics import make_scorer, mean_squared_error
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler, PolynomialFeatures
from sklearn.decomposition import PCA
from sklearn.linear_model import Ridge, Lasso, ElasticNet
from sklearn.ensemble import RandomForestRegressor, GradientBoostingRegressor, StackingRegressor
from sklearn.svm import SVR
from sklearn.cross_decomposition import PLSRegression
from sklearn.neighbors import KNeighborsRegressor
from xgboost import XGBRegressor
from lightgbm import LGBMRegressor
from catboost import CatBoostRegressor

# Générer des données fictives
from sklearn.datasets import make_regression
data = pd.read_csv("Challenge-20241125/data.txt", sep=" ")


y = data.iloc[:, 0]  # réponse
X = data.iloc[:, 1:].values  # matrice des prédicteursX_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# Division des données en apprentissage et validation
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.23, random_state=42)

# Scorer personnalisé pour le RMSE
rmse_scorer = make_scorer(lambda y_true, y_pred: np.sqrt(mean_squared_error(y_true, y_pred)), greater_is_better=False)

# Définir les modèles et les hyperparamètres
models = {
    'Ridge': (Ridge(), {'alpha': np.logspace(-3, 3, 7)}),
    'Lasso': (Lasso(), {'alpha': np.logspace(-3, 1, 5)}),
    'ElasticNet': (ElasticNet(), {'alpha': np.logspace(-3, 1, 5), 'l1_ratio': [0.1, 0.3, 0.5, 0.7, 0.9]}),
    'SVR': (SVR(), {'C': np.logspace(-2, 2, 5), 'epsilon': [0.1, 0.2, 0.5, 1]}),
    'RandomForest': (RandomForestRegressor(), {'n_estimators': [100, 200, 300], 'max_depth': [5, 10, 20, None]}),
    'GradientBoosting': (GradientBoostingRegressor(), {'n_estimators': [100, 200, 300], 'learning_rate': [0.01, 0.1, 0.2], 'max_depth': [3, 5, 7]}),
    'PCA + Ridge': (Pipeline([
        ('scaler', StandardScaler()),
        ('pca', PCA()),
        ('ridge', Ridge())
    ]), {'pca__n_components': [5, 7, 10], 'ridge__alpha': np.logspace(-2, 2, 5)}),
    'PolynomialFeatures + Ridge': (Pipeline([
        ('poly', PolynomialFeatures()),
        ('ridge', Ridge())
    ]), {'poly__degree': [2, 3, 4], 'ridge__alpha': np.logspace(-3, 2, 6)}),
    'PCR': (Pipeline([
        ('pca', PCA()),
        ('ridge', Ridge())
    ]), {'pca__n_components': [5, 8, 10], 'ridge__alpha': np.logspace(-3, 2, 6)}),
    'PLS': (PLSRegression(), {'n_components': [2, 5, 8, 10]})
    #'KNeighbors': (KNeighborsRegressor(), {'n_neighbors': [3, 5, 10, 20], 'weights': ['uniform', 'distance']}),
    #'XGBoost': (XGBRegressor(), {'n_estimators': [100, 200, 300], 'learning_rate': [0.01, 0.1, 0.2], 'max_depth': [3, 5, 7]}),
    #'LightGBM': (LGBMRegressor(), {'n_estimators': [100, 200, 300], 'learning_rate': [0.01, 0.1, 0.2], 'num_leaves': [31, 50, 70]}),
    #'CatBoost': (CatBoostRegressor(verbose=0), {'iterations': [100, 200, 300], 'learning_rate': [0.01, 0.1, 0.2], 'depth': [3, 5, 7]})
}

# Stacking (combiné de plusieurs modèles)
#stacking_estimators = [
#    ('ridge', Ridge(alpha=10)),
#    ('lasso', Lasso(alpha=0.1)),
#    ('svr', SVR(C=1, epsilon=0.1)),
#    ('xgb', XGBRegressor(n_estimators=100, learning_rate=0.1, max_depth=3))
#]
#models['Stacking'] = (
#    StackingRegressor(estimators=stacking_estimators, final_estimator=GradientBoostingRegressor()),
#    {'final_estimator__n_estimators': [100, 200, 300]}
#)

# Exécution de GridSearchCV pour chaque modèle
best_models = {}
for name, (model, param_grid) in models.items():
    print(f"Training {name}...")
    grid = GridSearchCV(model, param_grid, scoring=rmse_scorer, cv=18, n_jobs=-1)
    grid.fit(X_train, y_train)
    best_models[name] = {'best_params': grid.best_params_, 'rmse': -grid.best_score_}

# Résultats
results = pd.DataFrame(best_models).T
print(results)